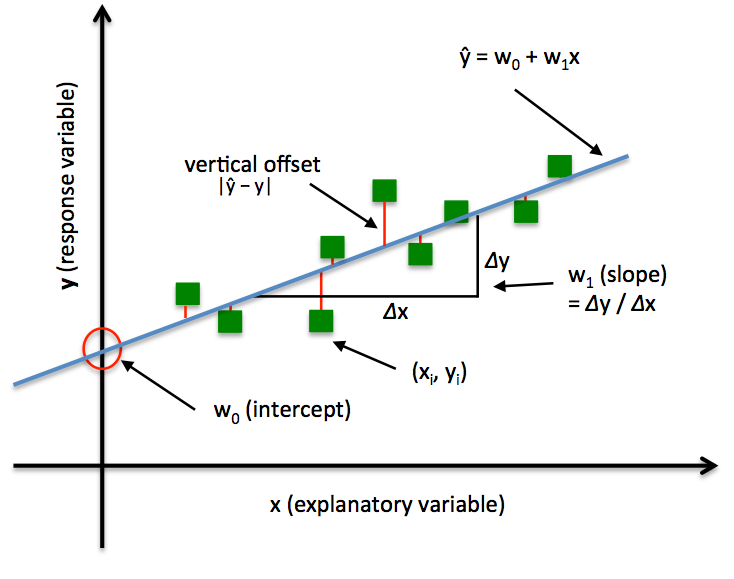
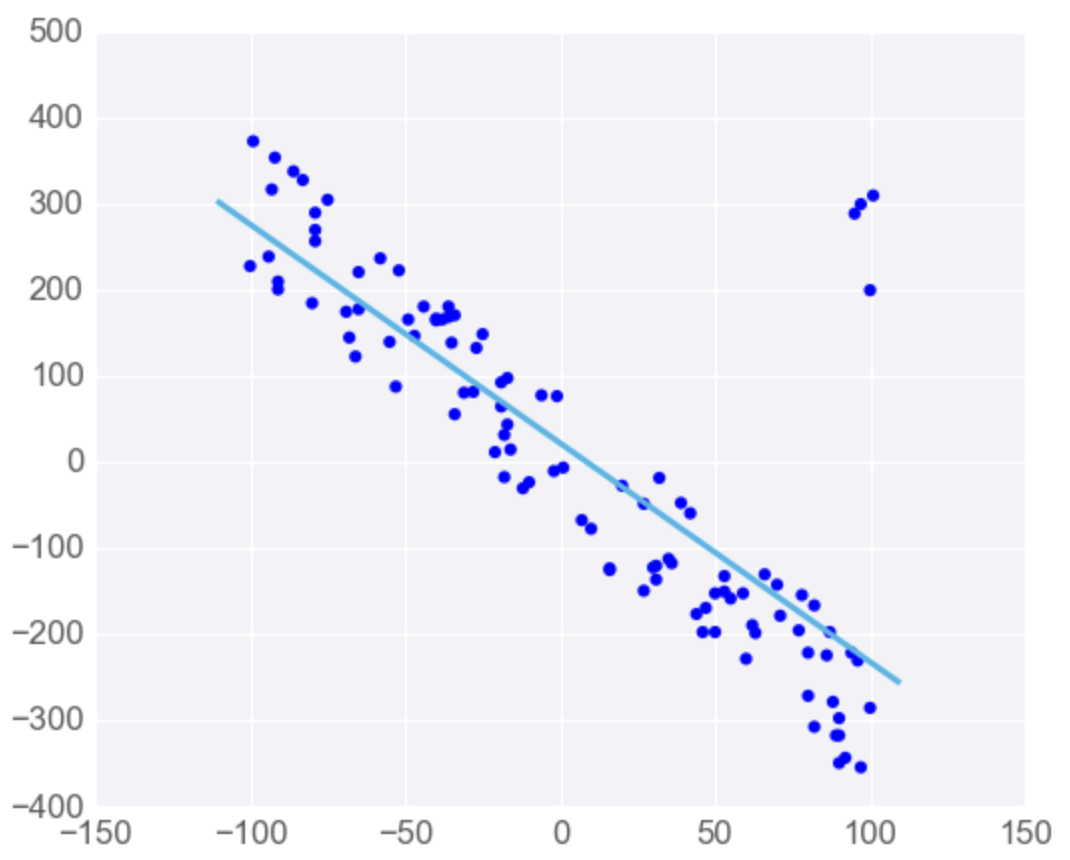
Closed Form Solution For Linear Regression
Closed Form Solution For Linear Regression - Web closed form solution for linear regression. I have tried different methodology for linear. The nonlinear problem is usually solved by iterative refinement; Assuming x has full column rank (which may not be true! Web one other reason is that gradient descent is more of a general method. Another way to describe the normal equation is as a one. Web i wonder if you all know if backend of sklearn's linearregression module uses something different to calculate the optimal beta coefficients. Web for this, we have to determine if we can apply the closed form solution β = (xtx)−1 ∗xt ∗ y β = ( x t x) − 1 ∗ x t ∗ y. Write both solutions in terms of matrix and vector operations. For many machine learning problems, the cost function is not convex (e.g., matrix.
Another way to describe the normal equation is as a one. Web 1 i am trying to apply linear regression method for a dataset of 9 sample with around 50 features using python. This makes it a useful starting point for understanding many other statistical learning. I have tried different methodology for linear. Web i wonder if you all know if backend of sklearn's linearregression module uses something different to calculate the optimal beta coefficients. Web closed form solution for linear regression. Then we have to solve the linear. Assuming x has full column rank (which may not be true! For many machine learning problems, the cost function is not convex (e.g., matrix. Web for this, we have to determine if we can apply the closed form solution β = (xtx)−1 ∗xt ∗ y β = ( x t x) − 1 ∗ x t ∗ y.
Web one other reason is that gradient descent is more of a general method. Assuming x has full column rank (which may not be true! Web 1 i am trying to apply linear regression method for a dataset of 9 sample with around 50 features using python. I have tried different methodology for linear. Another way to describe the normal equation is as a one. Web for this, we have to determine if we can apply the closed form solution β = (xtx)−1 ∗xt ∗ y β = ( x t x) − 1 ∗ x t ∗ y. For many machine learning problems, the cost function is not convex (e.g., matrix. Newton’s method to find square root, inverse. Write both solutions in terms of matrix and vector operations. This makes it a useful starting point for understanding many other statistical learning.
Getting the closed form solution of a third order recurrence relation
Assuming x has full column rank (which may not be true! Write both solutions in terms of matrix and vector operations. Web one other reason is that gradient descent is more of a general method. The nonlinear problem is usually solved by iterative refinement; Web it works only for linear regression and not any other algorithm.
matrices Derivation of Closed Form solution of Regualrized Linear
Web one other reason is that gradient descent is more of a general method. Then we have to solve the linear. For many machine learning problems, the cost function is not convex (e.g., matrix. Web for this, we have to determine if we can apply the closed form solution β = (xtx)−1 ∗xt ∗ y β = ( x t.
Linear Regression
Web it works only for linear regression and not any other algorithm. Web closed form solution for linear regression. Assuming x has full column rank (which may not be true! Web 1 i am trying to apply linear regression method for a dataset of 9 sample with around 50 features using python. Web β (4) this is the mle for.
Linear Regression 2 Closed Form Gradient Descent Multivariate
Then we have to solve the linear. For many machine learning problems, the cost function is not convex (e.g., matrix. Web i wonder if you all know if backend of sklearn's linearregression module uses something different to calculate the optimal beta coefficients. Another way to describe the normal equation is as a one. Web one other reason is that gradient.
SOLUTION Linear regression with gradient descent and closed form
Newton’s method to find square root, inverse. Then we have to solve the linear. I have tried different methodology for linear. Web β (4) this is the mle for β. Web for this, we have to determine if we can apply the closed form solution β = (xtx)−1 ∗xt ∗ y β = ( x t x) − 1 ∗.
Linear Regression
For many machine learning problems, the cost function is not convex (e.g., matrix. Newton’s method to find square root, inverse. Web closed form solution for linear regression. Web 1 i am trying to apply linear regression method for a dataset of 9 sample with around 50 features using python. Web for this, we have to determine if we can apply.
regression Derivation of the closedform solution to minimizing the
Web 1 i am trying to apply linear regression method for a dataset of 9 sample with around 50 features using python. Web closed form solution for linear regression. Web β (4) this is the mle for β. Write both solutions in terms of matrix and vector operations. Web it works only for linear regression and not any other algorithm.
SOLUTION Linear regression with gradient descent and closed form
For many machine learning problems, the cost function is not convex (e.g., matrix. Assuming x has full column rank (which may not be true! Then we have to solve the linear. Web one other reason is that gradient descent is more of a general method. Newton’s method to find square root, inverse.
SOLUTION Linear regression with gradient descent and closed form
Another way to describe the normal equation is as a one. Web closed form solution for linear regression. Then we have to solve the linear. For many machine learning problems, the cost function is not convex (e.g., matrix. Web β (4) this is the mle for β.
SOLUTION Linear regression with gradient descent and closed form
Web it works only for linear regression and not any other algorithm. Assuming x has full column rank (which may not be true! Web closed form solution for linear regression. Web one other reason is that gradient descent is more of a general method. For many machine learning problems, the cost function is not convex (e.g., matrix.
Web It Works Only For Linear Regression And Not Any Other Algorithm.
The nonlinear problem is usually solved by iterative refinement; Web closed form solution for linear regression. I have tried different methodology for linear. Write both solutions in terms of matrix and vector operations.
For Many Machine Learning Problems, The Cost Function Is Not Convex (E.g., Matrix.
Another way to describe the normal equation is as a one. This makes it a useful starting point for understanding many other statistical learning. Web β (4) this is the mle for β. Assuming x has full column rank (which may not be true!
Web 1 I Am Trying To Apply Linear Regression Method For A Dataset Of 9 Sample With Around 50 Features Using Python.
Web one other reason is that gradient descent is more of a general method. Then we have to solve the linear. Web i wonder if you all know if backend of sklearn's linearregression module uses something different to calculate the optimal beta coefficients. Newton’s method to find square root, inverse.