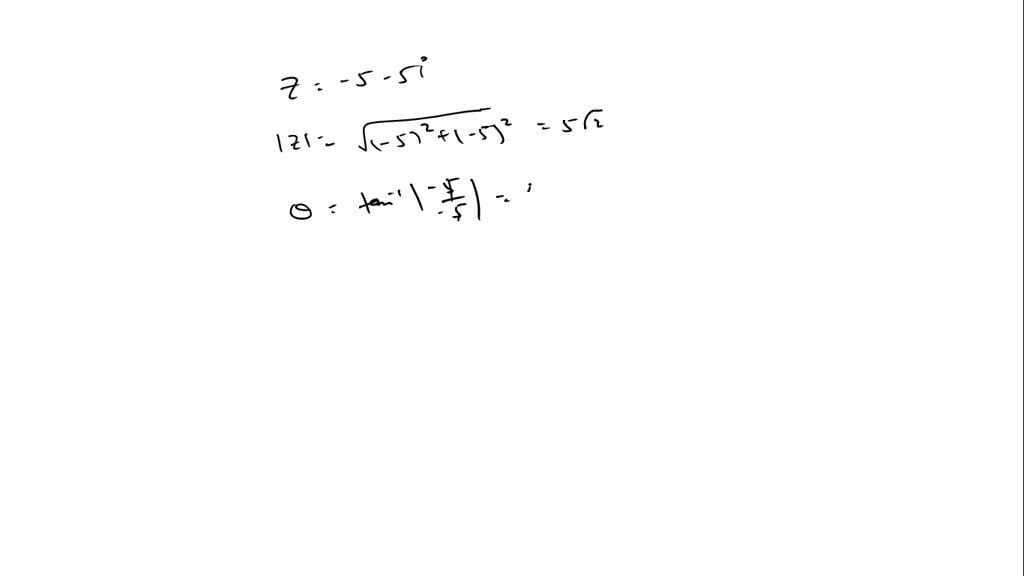Express The Complex Number In Trigonometric Form
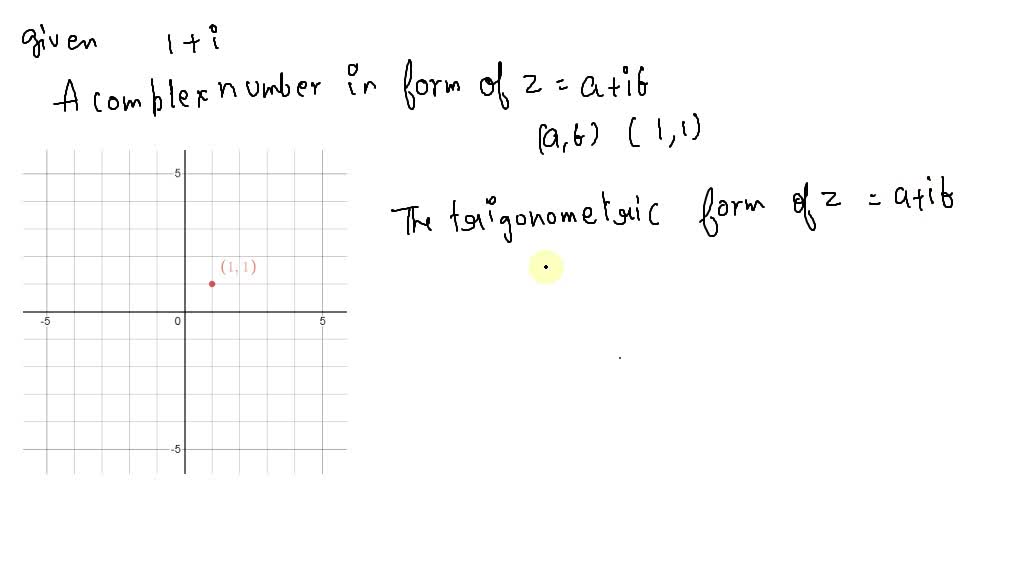
Express The Complex Number In Trigonometric Form - Given a complex number in rectangular form. Get this answer verified by an expert. Web how do you express the complex number in trigonometric form: How do you express the complex number in trigonometric form: Web how to write complex numbers in trigonometric form? Web this is the trigonometric form of a complex number where |z| | z | is the modulus and θ θ is the angle created on the complex plane. \(1−\sqrt{3}i\) to convert the following complex number from rectangular form to trigonometric polar. Web the trigonometric form of a complex number z = a + bi is = r(cos i sin ); Web how do you express the complex number in trigonometric form: To do this, we first determine the.
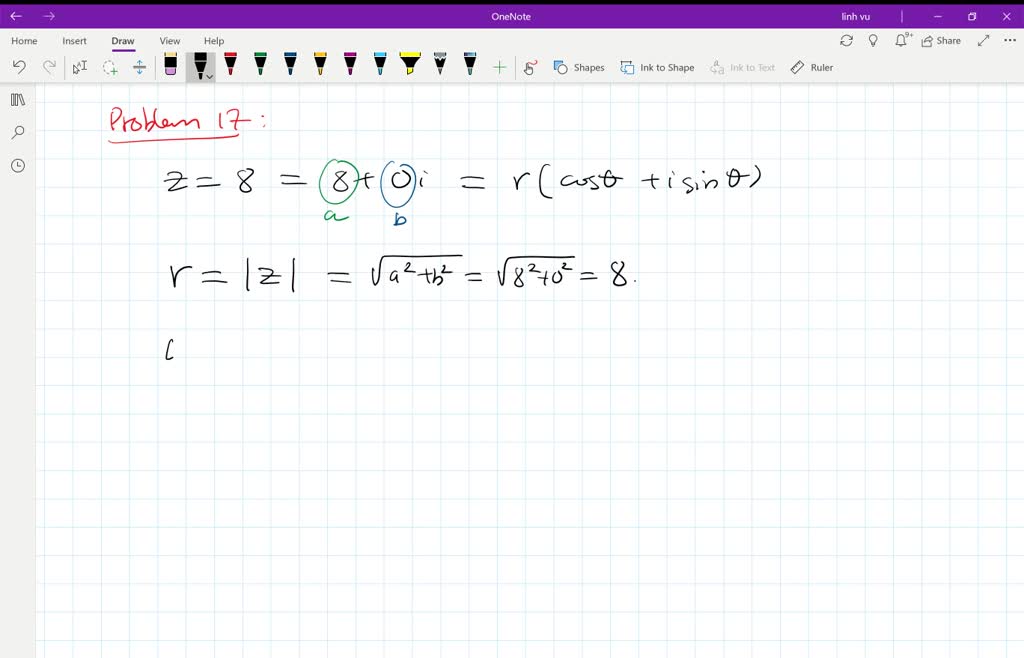
Z = a+ bi = |z|(cos(θ)+isin(θ)) z = a + b i = | z. Web how do you express the complex number in trigonometric form: Precalculus complex numbers in trigonometric form trigonometric form of. Get this answer verified by an expert. As a refresher, the distance between the origin and the complex number is equal to $|a + bi| = \sqrt{a^2 + b^2}$. Next, we must determine the argument θ. Here is the graph of 5 + 7 i. Web the polar form of a complex number expresses a number in terms of an angle \(\theta\) and its distance from the origin \(r\). Distributing to terms inside the (. Web the second chapter is devoted to the study of the trigonometric form of complex numbers and it contains two sections dealing with the following aspects:
Web how to write complex numbers in trigonometric form? \(1−\sqrt{3}i\) to convert the following complex number from rectangular form to trigonometric polar. To convert a complex number z to trigonometric form, we use the formula: Web the polar form of a complex number expresses a number in terms of an angle \(\theta\) and its distance from the origin \(r\). As a refresher, the distance between the origin and the complex number is equal to $|a + bi| = \sqrt{a^2 + b^2}$. Web represent the complex number 5 + 7 i graphically and express it in its polar form. Web how do you express the complex number in trigonometric form: Given a complex number, z = a + b i, we first compute the modulus, r = a 2 + b 2. Web the second chapter is devoted to the study of the trigonometric form of complex numbers and it contains two sections dealing with the following aspects: Z = a+ bi = |z|(cos(θ)+isin(θ)) z = a + b i = | z.
Trigonometric Form of a Complex Number Represent
Distributing to terms inside the (. Web this is the trigonometric form of a complex number where |z| | z | is the modulus and θ θ is the angle created on the complex plane. = b is called the argument of z. Web take the following complex number in rectangular form. \(1−\sqrt{3}i\) to convert the following complex number from.
6.5 Day 1 Trigonometric Form of a Complex Number YouTube
Where r = ja + bij is the modulus of z, and tan we will require 0 < 2. Web the second chapter is devoted to the study of the trigonometric form of complex numbers and it contains two sections dealing with the following aspects: This is the trigonometric form of a complex number where |z| | z | is.
Write each complex number in trigonometric form,
Web the answer you will get is: Web the cis form of the answer is just another way to write it ( cis(θ) is a symbol that is, by definition, equal to cos(θ) + isin(θ) ). This is the trigonometric form of a complex number where |z| | z | is the modulus and θ θ is the angle created.
📈Find the quotient of the complex numbers. Express your answer in
6 (cos (2pi/3) + i sin (2pi/3)) arrow right. To do this, we first determine the. Get this answer verified by an expert. Web this is the trigonometric form of a complex number where |z| | z | is the modulus and θ θ is the angle created on the complex plane. \(1−\sqrt{3}i\) to convert the following complex number from.
Express the complex number in trigonometric form
Here is the graph of 5 + 7 i. Web express the complex number in trigonometric form. Web your number, which is in trigonometric form, can be expressed in standard or rectangular form, z=a+ib, considering that: \(1−\sqrt{3}i\) to convert the following complex number from rectangular form to trigonometric polar. Web express the complex number in trigonometric form.
Express the complex number in trigonometric form. 2 2i
This is the trigonometric form of a complex number where |z| | z | is the modulus and θ θ is the angle created on the. \(1−\sqrt{3}i\) to convert the following complex number from rectangular form to trigonometric polar. Web how to write complex numbers in trigonometric form? Web your number, which is in trigonometric form, can be expressed in.
PPT Trigonometric Form of a Complex Number PowerPoint Presentation
This is the trigonometric form of a complex number where |z| | z | is the modulus and θ θ is the angle created on the. Web the second chapter is devoted to the study of the trigonometric form of complex numbers and it contains two sections dealing with the following aspects: Web take the following complex number in rectangular.
Complex Numbers in Trigonometric Form YouTube
Web represent the complex number 5 + 7 i graphically and express it in its polar form. Web the second chapter is devoted to the study of the trigonometric form of complex numbers and it contains two sections dealing with the following aspects: Web how do you express the complex number in trigonometric form: To do this, we first determine.
Trigonometric Form Into A Complex Number
Distributing to terms inside the (. Web the answer you will get is: Where r = ja + bij is the modulus of z, and tan we will require 0 < 2. Web how do you express the complex number in trigonometric form: Here is the graph of 5 + 7 i.
How do you express the complex number in trigonometric form 2+(sqrt 3
Web how to write complex numbers in trigonometric form? Z = a+ bi = |z|(cos(θ)+isin(θ)) z = a + b i = | z. Web the polar form of a complex number expresses a number in terms of an angle \(\theta\) and its distance from the origin \(r\). Here is the graph of 5 + 7 i. Given a complex.
Web Represent The Complex Number 5 + 7 I Graphically And Express It In Its Polar Form.
Web how do you express the complex number in trigonometric form: All of this can also be thought of in terms. Z = a+ bi = |z|(cos(θ)+isin(θ)) z = a + b i = | z. Web your number, which is in trigonometric form, can be expressed in standard or rectangular form, z=a+ib, considering that:
Precalculus Complex Numbers In Trigonometric Form Trigonometric Form Of.
To do this, we first determine the. Web the polar form of a complex number expresses a number in terms of an angle \(\theta\) and its distance from the origin \(r\). Next, we must determine the argument θ. R = 5 2 + 7 2 =.
A Few Ways To Express This Is:
Given a complex number, z = a + b i, we first compute the modulus, r = a 2 + b 2. \(1−\sqrt{3}i\) to convert the following complex number from rectangular form to trigonometric polar. Web this is the trigonometric form of a complex number where |z| | z | is the modulus and θ θ is the angle created on the complex plane. Web express the complex number in trigonometric form.
Web How Do You Express The Complex Number In Trigonometric Form:
As a refresher, the distance between the origin and the complex number is equal to $|a + bi| = \sqrt{a^2 + b^2}$. Choose the notation your class is using. Web the answer you will get is: Converting to polar from rectangular, x = 5 and y = 7.